MTBF Calculation

I offer reliable MTBF-calculations for Table of Content                                                    Goto MTBF knowledge page

• 1. General Remarks about MTBF or MTTF Calculation
• 2. MTBF Calculation for Electronics
  
• 3. MTBF Calculation for Mechanics
  
• 4. MTBF Calculation based on Bill of Materials
  
• 5. Calculating MTBF from Field Date correctly (!)
• 6. The foundation of MTBF Calculation
  
• 7. Further Reading (Links)
  

This is the MTBF calculation page. If you need to know MTBF for your equipment, you're absolutely right here. MTBF figures are needed, for example, for functional safety projects and for maintenance planning.

The difference between MTBF and MTTF is negligible in most cases, and very often it is just a matter of definition or convention. If you need to know the difference, just go to the MTBF page. From now on we will use the term MTBF only.


You are probably an R&D manager, or a development engineer, and you probably just happen to face some MTBF related issue, for example:

• the project specification has an MTBF requirement.
  
• This is quite likely for electronic equipment.
  
• your customer is asking for an MTBF figure
• your marketing department has heard about MTBF and wants to have it
  

There are many reasons why MTBF calculation has become an issue for you. Some are just nice to have, but many are real, for example:

• Someone needs MTBF just for marketing purposes. Then the only thing that matters is the MTBF figure, which then should be as high as possible. This would happen occasionally for electronic equipment.
  
• MTBF is needed for downstream calculations like
  
• expected maintenance / repair frequency and cost
  
• expected spares cost 
• # of required onsite spares needed in order to meet reliability / productivity / etc. requirements
• functional safety: safe failure fraction, probability of dangerous failure per hour for preferably electronics.
  

In 9 out of 10 cases when it comes to MTBF, we're talking about electronics, for which several recognized MTBF calculation standards exist. For mechanical equipment however, no such standards exist. We will discuss electronics first.

Up

2. MTBF Calculation for Electronics

Down

MTBF calculation for electronic equipment is usually performed with a recognized MTBF calculation standard. Most of the information needed is naturally given in bill of materials (BOMs). There are no specific requirements concerning BOM content and quality. The same BOM  you would give to your assembler will be fine.

Minimum information needed for MTBF calculation

• BOMs
• Calculation standard.
  
• List of MTBF calculation standards offered
  
• Environmental condition(s)
• For example: Ground mobile, ground benign controlled, airborne inhabited cargo, naval unsheltered, ...
• Ambient temperature range
  
• For example from -40°C to +85°C in steps of 5°C
  
• Temperature rise during operation (relevant for electronics, less relevant for mechanics.
  
• Keep this as simple as possible. In most cases, the same (average) delta T for all piece parts would be fine.
  In some cases, assigning individual dT for hot spots may be necessary. If components of the system are exposed to different environments / temperature(s), then, of course, components may be assigned individual dT.
  

From the above information I will be able to obtain reliable MTBF figures on PCB level and on overall system level. On piece part level, however, this approach will leave some or even many part type specific questions unanswered, therefore producing many uncertainties on piece part level. But fortunately this is only seldom an issue because, generally speaking, many uncertainties tend to cancel each other out.
As mentioned above, this approach is the de facto industry standard, and it is an interesting fact that the MTBF analyst doesn't need electrical schematics, the BOM only is just fine.
This does not mean that electrical schematics don't have useful information for MTBF calculation (in fact they have quite a lot), but it means that BOMs alone contain sufficient information for reliable MTBF figures on PCB and system level (but not on piece part level). This will become clearer if you read further.


Optional information for MTBF calculation

If MTBF figures on PCB and system level are not sufficient, and you also need reliable figures on piece part level, then the following information will be needed additionally. Please note that this approach will probably be more costly, and you probably would need it only for functional safety, military or aviation equipment (if at all).

• Individual dT for functional groups or even for every single piece part.
  
• This would have substantial effect on piece part MTBF, but only small effect on PCB and higher level MTBF.
  
• Useful / necessary only if there are big differences in dT among piece parts or among functional groups.
• Before getting tangled up in these details, consider limiting individual treatment  to a small number of piece parts, for example hot spots, and assigning average dT for all other piece parts.
  
  
• individual Stress levels (% of rating) for every single piece part.
  
• The minimum approach described further above would use 50% stress (voltage, power , current, depending on which applies) for all piece parts.
  
• Assigning individual stress levels would have substantial effect on piece part MTBF, but only small effect on PCB and higher level MTBF.
  
• Useful / necessary only if there are big differences in % stress among piece parts. 
• Before going this way,
  
• consider limiting individual % stress treatment  to a small number of piece parts, and assigning average % stress (not necessarily 50%) for all other piece parts, and,
  
• Before you start to find out all % stress values on your own, asking me for advice first would safe you a lot of unnecessary work!
  

Up

3. MTBF Calculation for Mechanics

Down

In contrast to electronics, there are no MTBF calculation standards available for mechanical equipment. Nevertheless there is an increasing demand for MTBF for mechanical equipment.
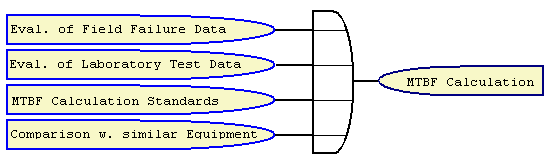
Field failure data, laboratory test data, and comparison with similar equipment may be eligible data sources for MTBF calculation. If asked, customers would often say that their field failure data is useless, and comparison with similar equipment won't work because of technological difference. But practical experience shows that the reality is almost always more favorable than customers would expect. For example, it often turns out that the field failure data is not so useless as it seems, or there is more information available than expected (e.g. from other departments), or the technological difference is less MTBF relevant than expected.
But even if customers were right with their judgment, it would still not spoil these data sources, because they may still be used as anchor points for (then seemingly more uncertain) MTBF estimations, which are often called "engineering judgment". But this would not be a pity at all, if communicated honestly, since most MTBF calculations are uncertain anyway, even when performed with a recognized MTBF calculation standard. The fact that no MTBF calculation standard is available for mechanical equipment doesn't add much additional uncertainty, but it rather makes the inherent uncertainty transparent. Finally, MTBF calculation is not only about math, statistics and engineering, but there is also a marketing aspect. For example, when the MTBF of the predecessor was 100.000 h, then the MTBF of the current item should not be less, should it? The VP marketing will probably have a say here.

What most engineers must learn about mechanical MTBF is the fact that probably a reasonable guess (often called engineering judgment) may be a valid data source, because it is very often the only possible way. Engineers must learn to make valid guesses.

In my career I was able to guide many customers to valid MTBF judgments, which they were confident to defend and  to communicate to their customers.

Some readers may point to NPRD 1995, 2011 and 2016, which are publicly available failure rate catalogs (not calculation standards) for mechanical components. However, despite being a kind of "holy grail" in aviation and other industries, these catalogs often raise more questions than they would answer. Picking the right data set is often just like gambling. For example, if you need to have a certain MTBF figure not less than one million hours, you will probably find a satisfactory data set.

Up

4. MTBF Calculation based on BOMs

Down

While MTBF is more intuitive, failure rates are easier to handle: Failure rates can be just summed up in order to obtain a sum of failure rates, but summing up MTBF would give apparently nonsensical results.

As already mentioned further above, MTBF calculation for electronic equipment usually means that a recognized MTBF calculation standard is used. Most of the information needed is naturally given in bills of material (BOMs).
MTBF calculation standards can be conceived as sets of mathematical formulas where each electronic piece part type (resistor, capacitor, ...) has its own dedicated formula. For example, the formula for ceramic capacitors produces the failure rate for a ceramic capacitor under certain (electric and environmental) conditions. To give an idea, the following overly simplified example may help:
Failure rate of a metal film resistor = power rating [W] x relative power stress [%] / temperature [°C].

Below list describes the steps of MTBF calculation based on BOMs.
I can assist you on any of these steps:

1. Chose the MTBF calculation standard.  
2. Define global parameters, e.g. ambient temperature and environment. 
• Your design engineer, maintenance technician, or the requirements specification may provide this information.
  
3. Identify all local parameters for every piece part and calculate all piece part failure rates.
   
• That's my job.
  Each piece part type has its own specific set of parameters, for example, capacitance for capacitors, # of transistors for linear ICs, diode type (schottky, suppressor, general-purpose, ...)
  
4. Sum up all piece part failure rates, calculate MTBF = reciprocal of the sum of piece part failure rates, and create the MTBF report . 
• That's my job, too.
  The report will contain (among many other information) failure rate and/or MTBF figures on PCB and system level for a range of temperatures (e.g. from -40°C to +85°C in steps of 5°C), and on piece part level for one selected temperature.  If you need more, just let me know.
  

MTBF figures on PCB and system level may differ substantially depending on the MTBF calculation standard, all other factors being equal. A difference of factor of 3 on PCB level is quite normal, and even factor 10 is possible.
The reason is that these standards have been established under different circumstances and with different goals. More information on this can be found at the bottom of the MTBF page.
On piece part level, the difference may be even worse for specific parts, where factor 100 or even higher may certainly happen from time to time. But this is irrelevant as long as you are interested only in PCB level and system level MTBF.

Only in rare cases would  MTBF figures on piece part level considered necessary, for example in functional safety. Then, step 3. (local parameters) in the above list becomes more work-intensive because someone must identify stress levels and temperatures for all piece parts. The good news is that I can show you how to get this done efficiently. 
But, again, provided that there is no strong reason against it, I recommend that MTBF calculations be performed with average stress and temperature figures for every piece part.

Why do average temperature and stress figures on piece part level still produce reliable MTBF figures on PCB and system level? There are two reasons:

1. One reason is just a statistical effect: If many independent uncertainties with two possible directions (too low / too high) are summed up, the result will not be a high, but rather a small uncertainty, probably even smaller than the highest single uncertainty. 
   This is just a simplified description of the so-called central limit theorem, which belongs to the foundations of general statistics.
   
   
2. The other reason comes from the MTBF calculation standards themselves.
   As mentioned above, MTBF calculation standards are basically sets of mathematical formulas, whose parameters have been derived from comprehensive field failure data. Nevertheless, each standard has at least a few part types for which only limited field failure data was available, therefore resulting in rather coarse formulas that wouldn't take into account parameters that otherwise would be considered important, for example temperature and stress. The point is that these formulas tend to produce rather high failure rates, and therefore these part types tend to affect the PCB and system MTBF disproportionably.
   

Up

5. Calculating MTBF from Field Failure Data correctly

Down

This paragraph applies for laboratory test data, too.

Calculating MTBF from field or laboratory data just by dividing the cumulative operating hours by the number of fails seems intuitive, but unfortunately this is wrong. Even worse, it would produce optimistic figures, which can be dangerous if communicated to customers.
Attentive readers may suspect that dividing by the # of fails cannot be correct for the simple fact that it doesn't work for zero failures. This is even more interesting because zero failures data sets are encountered quite often, in particular when the cumulative operating hours is smaller than the (unknown) MTBF, or a test is too short to produce a failure.
The actual reason however is that it ignores the random character of failures, and instead implicitly assumes the failures somehow to occur according to a (predictable) timetable. The fact that failures (should) occur randomly is explained in depth on the MTBF page. The reason why results become optimistic is more difficult to grasp, and maybe the following example may help a bit:

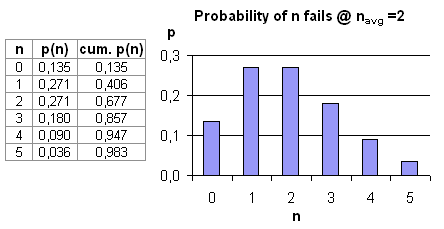Suppose the real MTBF was 500 h. Then the average outcome of a 1.000 hour test would be 2 failures. Due to statistical variation however, the outcome of a specific  test may be 0, 1, 2, 3 or 4 failures, and even 5 and more cannot be ruled out, but if repeatedly tested, 2 failures would be the average.
Now suppose you don't know the real MTBF, therefore you perform a 1.000 h test, and the outcome is 2 failures. What would be the best and honest guess for the MTBF based on the given information, which is only the test result? Here comes the poisson distribution into the game. The picture shows the probability of n failures occurring in a 1.000 h test provided that the average # of failures would be 2 (which equals MTBF = 500 h). Notice the following:

• The probability for up to 2 failures is substantially higher than 0,5 (0,677).
  

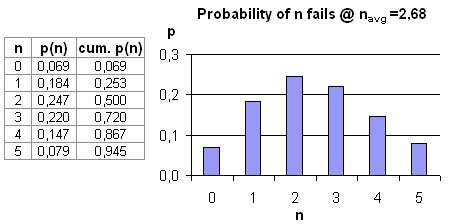This means: If 2 failures are encountered in a 1.000h test, the real MTBF would be rather smaller than 500h, and therefore the best guess would be some figure below 500 h. By playing with the poisson distribution, we find that if the average # of failures was 2,68 instead of 2, the probability of up to 2 failures in any specific selected test would be 0,5.
Therefore, if we don't know the real MTBF figure, and our 1.000 h test produces 2 failures, the best guess for the average number of failures within 1.000 h would be 2,68, which transforms into the best guess MTBF = 1.000h / 2,68 = 373 h.

Note that randomness (failures occurring randomly) is the cause for this. It's not a statistical issue, and in particular it has nothing to do with statistical confidence.
Of course, an exact mathematical formula exists, so we don't need to iteratively reverse-calculate MTBF with the Poisson.   More information on this can be found on the MTBF page.

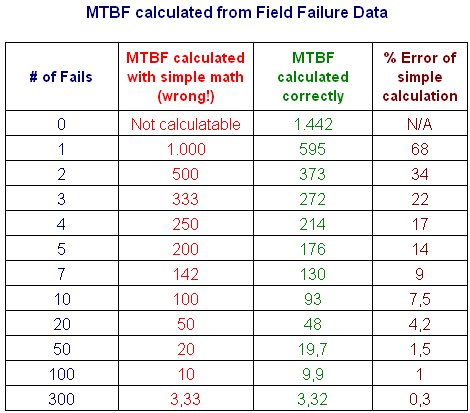
The table below shows calculated MTBF for a wider range of # of failures. You may use it to estimate MTBF from field failure data or from laboratory test data. In order to keep the table simple, the underlying cumulative operating time (or test duration) is always 1.000 h. MTBF for any other cumulative operating time can be obtained by simple linear conversion.
Please note:

• MTBF figures are rounded down, which is common practice in safety engineering.
• MTBF figures have 50% (upper and lower) statistical confidence.
  
• 50% statistical confidence means the same as if no statistical confidence was specified.
  

Up

6. The Foundation of MTBF Calculation?

Down

This paragraph aims to make the MTBF calculation topic complete, from the perspective of someone who is rather interested in how MTBF calculation works, than in the theoretical background of MTBF (which is described in much more detail on the MTBF page).

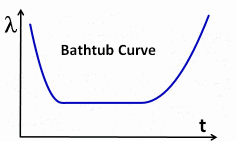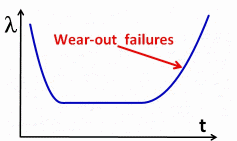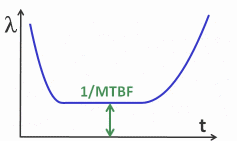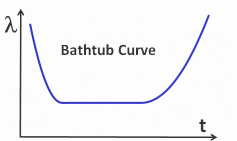
While MTBF is perceived as an intuitive metric, its underlying theory is actually a bit complex in that sense that it addresses multiple (seemingly uncorrelated) aspects at the same time. A good starting point is the so-called bathtub curve, in particular the middle part.

The middle part of the bathtub curve has a constant failure rate. With MTBF ~ 1/ failure rate, the MTBF is constant in the middle part.
Constant failure rate is not just a simplification. The mathematical property

• constant failure rate

is the same as the phenomenological property

• failures occur randomly

If all failures occur randomly, then no failure would occur systematically, therefore all failures would be unpredictable, and finally no means would exist in order to prevent failures.
This looks like an idealization at first glance, but nevertheless does it perfectly describe companies doing everything within their power in order to deliver flawless products to customers. Such products would be free of foreseeable failures, and all remaining failures that would still occur, would be attributed to force majeure, because no means exists that would prevent such failures.

1. If failures occur only randomly, preventive maintenance would have no effect, because prevention would need predictability.
   
   
2. Constant failure rate means that the product doesn't age. Regardless of how long the product has been in operation: as long as there is no failure, the product is always like new. This is because due to future failures being unpredictable, past failures wouldn't deliver any information for the prediction of future failures. In other words, the failure history of a product doesn't tell anything about future occurrences of failures. The only thing the failure history does tell us is the failure rate.
   More generally put: As long as products don't fail, they can be considered as new products regardless of the time already spent in operation. 
   
   
3. The constant failure rate property turns out to be useful if field failure data is limited. In this case, the constant failure rate property turns into a helpful assumption because the model requires less information than any other model with changing failure rate. In many cases, assuming constant failure rate is the only way at all to establish a failure rate model.
   The constant failure rate model needs only this information:
• Cumulative operating time of the population of units,
• # of failures during that time.  

          The constant failure rate model does NOT need:

• the time points when the units failed,
  
• the individual operating times of the units.
  

If you don't need time points and individual operating times, the field failure information you once considered useless suddenly becomes eligible for MTBF calculation.
Note that this is not a "trick", but rather making existing information accessible.




In practice however, by far not every piece part failure would result in a system failure, and even more, some failures wouldn't have any noticeable effect at all. This is true even for "simple" (= neither redundant nor otherwise fault tolerant) systems, for example drift of some resistors and some capacitors, and even the total loss of some capacitors.
For such systems, the serial model turns out to be a bit pessimistic. But this is no pity, and in safety context it is even welcome.
However, for redundant or otherwise fault tolerant systems, the serial model would give terribly pessimistic MTBF because it would ignore the redundancy and fault tolerance properties. For such systems, MTBF (or failure rate) calculation would be applied only on piece part and on functional group level, while for the system MTBF more dedicated calculation methods like fault tree analysis, reliability block diagrams or markov analysis would be preferred.
MTBF figures on functional group level would then serve as quantitative input for these methods.

Up

7. Further Reading

To top

• Overview of reliability and safety analysis methods
  

• More information about MTBF
  

• Functional Safety