Weibull Analysis

Weibull analysis is based on the so called Weibull distribution (from now on called "the Weibull"). The Weibull is used for modeling failure rate  versus time. It is interesting that in this context, the Weibull serves only as a heuristic distribution function without any mathematical foundation. Nevertheless, the Weibull has proved to be useful in practice because it can model failure rate over time quite well.
Today, the name Weibull analysis is used synonymously with the type of analysis described here, regardless of the distribution function actually used (e.g. the log-normal distribution or the beta distribution).

Originally, Weibull analysis used to be a purely graphical method for determining failure rate over time, because at that time there wasn't any software available.
An essential feature of Weibull analysis is the specific axis scaling of the so called Weibull plots. This scaling ensures that cumulative distribution functions appear as a straight line, and not  as an S-curve. Straight lines facilitate assessment by human eye. Today there are plots available not only for the Weibull, but also for other distribution functions.
 
If the failure data build a straight line (at least approximately), then the underlying distribution function of the data does follow the distribution function of which the Weibull plot is made.
The parameters of the distribution function, namely the average life and possibly a further parameter ("shape"), can be determined directly from the straight line (by human expert eye).
 
Despite today's availability of specific Weibull software, experts won't set aside human eye assessment. Therefore, today's Weibull software still provide these "old fashioned" graphical Weibull plots.
 
The most important distribution function in Weibull analysis is the Weibull distribution. This, as well as Weibull analysis in general, goes back to Mr. Waloddi Weibull.

The two parameters of the Weibull distribution are:

1. Characteristic life (statistically just an average),
2. Shape factor

As indicated above, the Weibull distribution is a heuristic engineering tool, because it can model failure rate over time quite well. Therefore it is not a mathematically established distribution function. Changing failure rates over time are usually a consequence of wear and changing operating conditions.

The characteristic life is the average life time of the items of the population until they fail.
The shape tells us whether all items share approximately the same life time (and therefore fail within a small time window), or whether their life times differ significantly.
The latter case would be unfavorable from a maintenance viewpoint, since individual failures would be difficult to forecast.

It is a unique characteristic of Weibull analysis that the failure data must be entered into a specially scaled coordinate system (Weibull plot), so that the data can build a straight line. In addition, there are specific rules how the data is to be entered. Then, both parameters (characteristic life and shape) can be read directly from the straight line by human eye.
Even if the data don't make a straight line, experts can make particular conclusions:

• changing operating conditions at a specific point in time in the past
  
• two or more (instead of one) sub-population (e.g. items coming from two different production lines)
  
• ...
  

The following figure shows a completed Weibull plot:


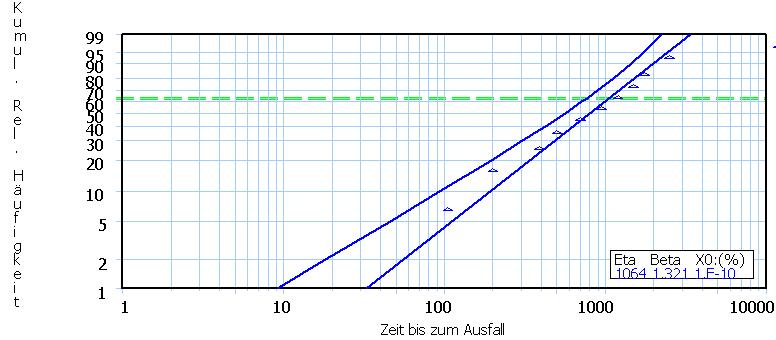Triangle: A data point (a failure).
Left perpendicular axis: Relative failure frequency in % (double-logarithmic scale). For example, 99 means that 99% of the population have failed.
Horizontal axis: Time (logarithmic scale).

The placement of the triangles follows dedicated statistical procedures and is therefore beyond this introduction.
The plot shows 10 data points (triangles) in total, the last being close to 100%. Therefore the total population consisted of 10 items accordingly.

Example:
Leftmost triangle: The first failure happened after a little more than 100 hours; the cumulative incidence was registered not at 10% (because 1 out of 10 = 10%), but statistically correct at about 7%.

The blue straight line is calculated by the Weibull software, however, it is approximately what would be concluded by human expert eye. The blue curve on the left is the statistical left 90% confidence bound of the straight line, i.e., the true straight line lies pretty sure on the right of this curve.

The intersection of the straight line with the green dashed line (at 63%) yields the characteristic life Eta, here a little more than 1000 hours.
The shape Beta (1,321) can not be derived from this Weibull plot because, fore the sake of simplicity, a few plot elements (the so called "pole") have been omitted. Complete Weibull plots however would also allow the reading of Beta.