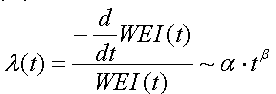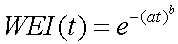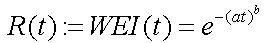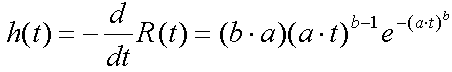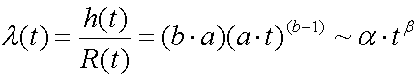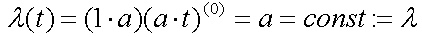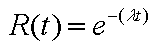Modeling Reliability with the Weibull Distribution Function

You are here:

Page Content

1. The Weibull

Down

The Weibull distribution function is often used in reliability analysis, which is often called weibull analysis.
The Weibull distribution function is very common in reliability analysis because its failure rate follows a power law:

With the power law we have a simple yet efficient vehicle in order to model various failure vs. time behavior The so called bathtub curve, which consists of the following three phases, is a good example:

decreasing failure rate (beta < 0)
constant failure rate (beta = 0)
increasing failure rate (beta > 0)

The Weibull distribution function can be expressed in the following general way; it is basically an exponential function with the exponent raised to a power:

Now we prove that the Weibull has the stated properties. In the Weibull reliability model, R(t) becomes WEI(t).

Here we substituted (ba)(a)^b-1 by alpha and (b-1) by beta.

For the constant failure rate case, we set b to 1, and obtain

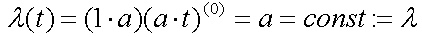
and accordingly:

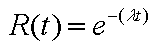
The weibull distribution plays a vital role in extreme value statistics, where it describes the distribution of max and min values of samples. The Weibul has been introduced into the reliability world by the swedish engineer Waloddi Weibull ("Y-Bull"). The Weibull is so important, that reliability analysis, even when using some other distribution function, is often called weibull analysis.
In reliability analysis, apart from the constant failure rate case (b=1 --> beta=0), the Weibull is (only) a (admittedly useful) engineering vehicle with no mathematical foundation. This means, the Weibull is used for the only reason that it works well in practice.
Therefore, stating that something follows a Weibull distribution is incorrect. Instead, it is better to state that something can be satisfactorily modeled with the Weibull.
The weibull is a common model for describing aging and wear-out processes.
The constant failure rate case however is built on solid mathematical foundation, in other words, it exactly describes certain mechanisms occurring in nature. More on this can be found on the MTBF page.

2. Weibull Shape Factor

Down

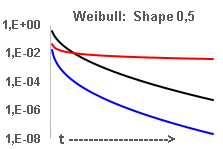
The diagrams below show R(t), h(t) and Lambda(t) for the Weibull for b values ("shape") between [0,5 ... 3,0], and a fixed value for a ("scale"). b = [ 0,5 ... 3,0] covers almost all practical cases.
As mentioned before, the hazard rate h(t) is not important, but is still shown for didactical reason.

Bigger and more detailed diagrams:

The vertical scale is "true" for all three graphs R(t), but "meaningful" only for R(t).
Both axes are linear
The horizontal axes are the same for all diagrams

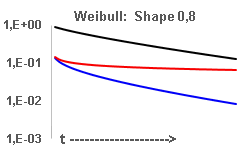
Smaller diagrams:

Vertical axes are logarithmic
The purpose is to show the behavior for t--> 00, which is a bit tricky with the toolset provided by MS Excel. Therefore the range of the horizontal axes vary with the Weibull shape factor.

2.1 Infant Mortality

Down

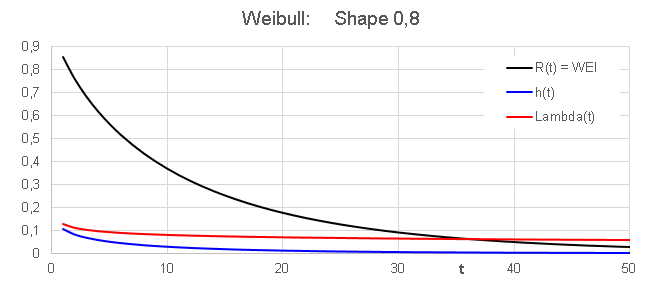
The first out of three phases in the bath tub curve is called early failure phase or infant mortality phase.

This phase is characterized by a decreasing failure rate Lambda(t)

-- > Weibull with shape factor < 1

Customers should not be exposed to this phase.

More on the bathtub curve can be found on the bathtub curve page
More on the three phases of the bathtub curve can be found on the MTBF page.

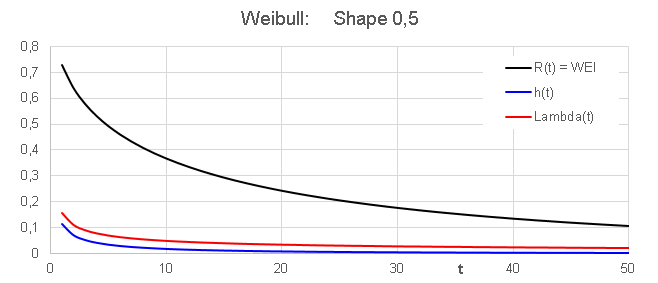
Note that all three graphs, R, h and Lambda, are monotonically decreasing functions with time.For t--> 00, all three tend asymptotically to zero. It looks like as if the graphs tend to zero with different "speed", but this is meaningless. The graphs reperesent different things, and sould therefore not be compared to each other.

2.2 Useful Product Life Phase, Random Failures

Down

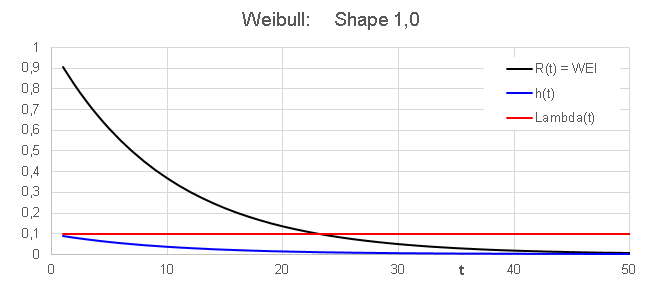
The second out of three phases in the bath tub curve is called useful product life phase . Weibull shape =1

This phase is characterized by a constant failure rate Lambda(t)

-- > Weibull with shape factor = 1

Customers should be exposed only to this phase.
The constant failure rate case is actually a strong achievement every supplier and manufacturer should strive to.

More on the bathtub curve can be found on the bathtub curve page .
The Weibull with shape factor 1 is also called Exponential. The exponential distribution is the foundation of the powerful concept of MTBF. Much more on this, in particular the consequences and implications of constant failure rate, can be found on the MTBF page.

The Weibull with shape factor 1 and the Gamma with form factor 1 are identical distribution functions.
The Gamma plays a role in reliability analysis too:
Gamma_k describes how long it takes for k random events to occur.
--> The Gamma₁ = Exponential describes how long it takes for 1 random event to occur.

2.3 Wear-Out Phase

Down

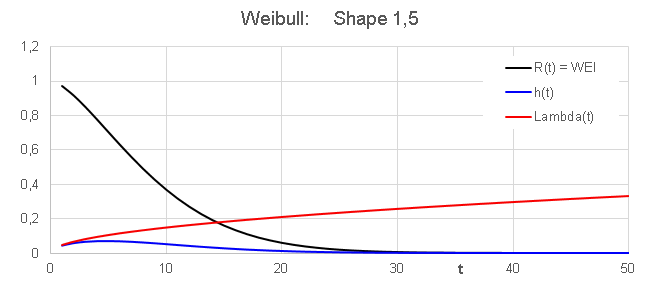
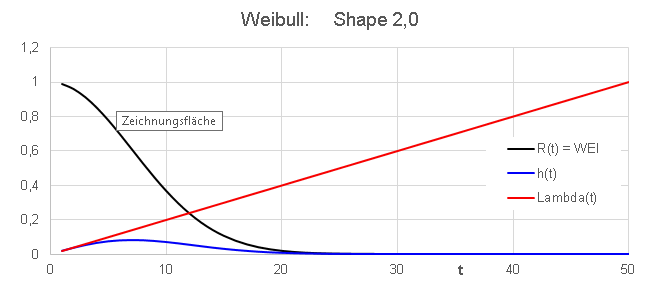
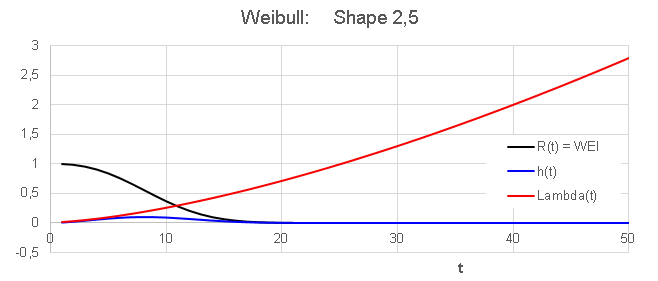
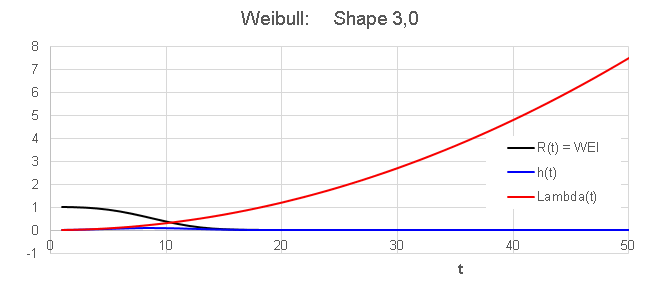
The third out of three phases in the bath tub curve is called wear-out phase. 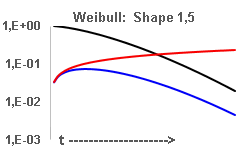Weibull shape >1

This phase is characterized by a increasing failure rate Lambda(t)

-- > Weibull with shape factor > 1

Customers should not be exposed to this phase.

More on the bathtub curve can be found on the bathtub curve page
More on the three phases of the bathtub curve can be found on the MTBF page.

R(t) and h(t) are monotonically decreasing functions with time.For t--> 00, h(t) and Lambda(t) tend asymptotically to zero. It looks like as if the latter two tend to zero with different "speed", but this is meaningless. The graphs reperesent different things, and sould therefore not be compared to each other.

Lambda(t) is a monotonically increasing function with time. In fact, lambda tends to infinity for t--> infinity. In order to make this appear not too weird, we just need a population of infinite size. Mathematitians would see no reason to bother. For the reliability engineer however it is clear that the failure rate Lambda would increase only as long as there are units that can fail, but as soon as the last unit of the population has failed, Lambda would suddenly drop to zero.

The Weibull with shape factor 2 is also called Rayleigh. Simply put, the Rayleigh distribution can be conceived as the integral of the two dimensional Normal distribution. However, this is meaningless in reliability analysis.

To top

Next Topic