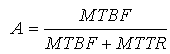A simple Introduction into Reliability Metrics

Failure Rate, MTBF, Reliability, and Availability

You are here:

Page Content

1. MTBF

Down

The most common (and also mostly misunderstood) reliability metric ist the MTBF, mean time between failure. MTBF has by no means any relationship with lifetime. The table below shows some MTBF figures originating from an earlier version (mid 1990s) of the Telcordia SR 332 MTBF calculation standard. Therefore, the figures are quite dated.

Assembly	MTBF [h]
Personal computer	2.000
Computer-hard-disk-drive	15.000 As of 2022, HDD manufacturers would communicate MTBF figures of 1.000.000 h or even higher.
Computer mouse	100.000
Computer keyboard	25.000
Computer-color-monitor	8.000
Computer CD ROM drive	8.000

The table suggest that more complex devices tend to have lower MTBF compared to less complex devices. This is generally true, and in particular, MTBF can be viewed as a kind of complexity metric. More information on this can be found on the MTBF page.

MTBF is a statistical metric characterizing a population of units. In order to illustrate this, we use the computer mouse in the above table. MTBF = 100.000 h does not mean that a specific mouse would fail every 100.000 h (not even on average), but if we consider, for example, 1.000 computer mice, we would expect a mouse failure every 1.00.000 cumulative operating hours on average, which is 1 mouse failure every 100 calendar hours on average ( ~ 4 calendar days). Since the MTBF concept comes with constant failure rate over time, we would expect the first mouse failure on the first few days, on average on the 4th day, to be precise. More on constant failure rate, in particular it's implications, can be found on the MTBF calculation page.

In order to understand the MTBF concept even better, and in particular to show the difference to lifetime, we consider the following, "extreme" examples:

    Rifleman, bullet:
    A rifleman shoots 1000 bullets onto a target. The flight time of the bullet shall be 0,5 seconds.
    We assume that 2 out of 1000 shots would not work properly due to failures related with the bullet.
    --> The lifetime of a bullet is 0,5 seconds.
    --> MTBF = (1000 x 0,5 s) / 2 = 250 seconds.
    --> MTBF is substantially higher than lifetime. This is generally true for units with low complexity.

    Computer center with many servers:
    A computer center is running nonstop with 1 failure per month on average. The design life of the servers shall be 10
    years.
    --> Server lifetime = 10 years, therefore the lifetime of the computer center is also 10 years.
    --> MTBF = 1 month.
    --> MTBF is substantially lower than lifetime. This is generally true for units with high complexity.

Conclusion:

MTBF and lifetime are different metrics with no relationship between each other.

The difference can be seen in the bath tub curve quite clearly.

MTBF is a statistical value that applies to a population of units, and not to a single specific unit.

Remark: Both above conclusions are true in more than 99% of all cases. In order to keep this introduction simple, we will not dig into the remaining 1% here. More information on this can be found on the MTBF page.

There are more interesting aspects about MTBF, but since we want to keep this introduction simple, we will not cover them here.

2. Failure Rate

Down

The failure rate is just the reciprocal of the MTBF.
In general, a rate is a number of occurrences per time unit.
--> Failure Rate = Number of failures per time unit.

Common time units are 1.000.000 hours (then expressed in units of failures per million hours, fpmh) and 1.000.000.000 hours (then expressed in units of failures in time, Fit).

Using failure rates instead of MTBF, the above computer equipment table would look like this:

Assembly	MTBF [h]	Failure Rate [fpmh]	Failure Rate [Fit]
Personal computer	2.000	1E6/2.000 = 500	1E9/2.000 = 500.000
Computer-hard-disk-drive	15.000	1E6/15.000 = 66,7	66.700
Computer mouse	100.000	10	10.000
Computer keyboard	25.000	40	40.000
Computer-color-monitor	8.000	125	125.000
Computer CD ROM drive	8.000	125	125.000

We will learn more about failure rate in a later failure rate paragraph.

3. Availability

Down

Both MTBF and failure rate just tell us "how often" units would fail. Sometimes however we would not so much be interested in the number of failures, but rather in the percentage of time the unit is in an oparable condition.
The comoputer center described above is a good example. One failure per month, or even many failures per month, may be tolerable as long as the downtime remains sufficiently short. Therefore, Availability would be the appropriate metric:

Availability is the probability that an item will be operable

under stated conditions
for a stated period of time

The most simplistic formula for Availability A is just uptime divided by total time:

MTBF is the mean time between failure and MTTR is the mean time to repair.
MTTR ( = downtime) is the average time needed to perform a repair.

Availabiloity denoted as above is the so called "inherent" or "intrinsic" availability.
We will learn further (and more realistic) formulas for availability in a later availability paraghraph.

Conclusion:
When uptime matters first, the number of failures per time is less important. In particular:

The failure rate of a unit may be high, but if at the same time the repair time is sufficiently low, the availability may still be acceptable (= sufficiently high).
The other hand, ailure rate of a unit may be low, but if at the same time the repair time is too high, the availability may still be unacceptable (= too low).

4. Reliability

Down

Reliability is the probability that an item will perform

a required function without failure
under stated conditions
for a stated period of time.

The phrase "without failure", which actually makes the difference to availability. Hence, Reliability could also be expressed as the probability of survival. The focus of reliability lies clearly on the non-occurrence of failures, therefore, reliability is the metric of choice when interruption of operation matters. Common examples are military missions and flights.
We will learn more about reliability in a later reliability paragraph.

To top

Next Topic